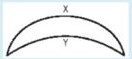
Q. In the below figure, the two circular curves create 60° and 90° angles with their respective centers. If the length of the bottom curve Y is 10π, find the length of the other curve.

A. \(\frac{15π}{\sqrt{2}}\)

B. \(\frac{20π\sqrt{2}}{3}\)

C. \(\frac{60π}{\sqrt{2}}\)

D. \(\frac{20π}{3}\)

E.  \(15π\)

A. \(\frac{15π}{\sqrt{2}}\)

Join the endpoints , let X1 and Y1 be the respective centers.

Given that length of Y is 10π and angle subtended is 60°

\(\Rightarrow \frac{60}{360} \times  2 \pi r = 10 \pi \), where r is the radius.

⇒ r = 30

Triangle AY1B is an equilateral triangle ⇒ AB = 30 units

In 45-45-90 triangle AX1B,

\(AX_{1}\) = \(BX_{1} = \frac{30}{\sqrt{2}}\)

= \(15\sqrt{2}\)

Now, length of arc X = \(\frac{90}{360}×2π×15\sqrt{2}\)

= \(\frac{15π}{\sqrt{2}}\)